Sorting (Part 7.0): Merge Sort

Hello everyone! This is part 7.0 of my Sorting series. I know, I said last time that there would be a 6.1, but not just yet!

So, anyway, here we are at 7.0 -- and I'm wondering about how long I can drag this whole thing out...

Merge Sort: The Algorithm Under the Hood

Merge Sort (Wiki) is another divide and conquer algorithm, much like Quick Sort.

One big difference from Quick Sort is that Merge Sort doesn't pick any special pivot. Rather, Merge Sort splits the array-to-sort arr right down the middle. Then, it uses recursion to Merge Sort the left = arr[0..k] and right = arr[k+1..n-1].

It 'll continue splitting each piece of the array-to-sort arr into smaller and smaller pieces, until the pieces are of size two or less.

That's the wonder of divide and conquer: take a daunting problem and split it into a lot of smaller, more manageable tasks.

So, we get to very small arrays that essentially follow this pattern: arr[a..b], where 0 <= a <= n - 2, 1 <= b <= n - 1, and b - a <= 1, meaning that the array piece arr[a..b] has a length of two or less.

Okay, so now we have a bunch of arrays that are two-or-less elements in length. Two or less elements can mean one of three things:

1. There are no elements in the array, so we return it move on to the next piece.
2. The array has one element, so we return that and move on.
3. The array has two elements. Here, we swap the elements if they're out of order, and then return it.

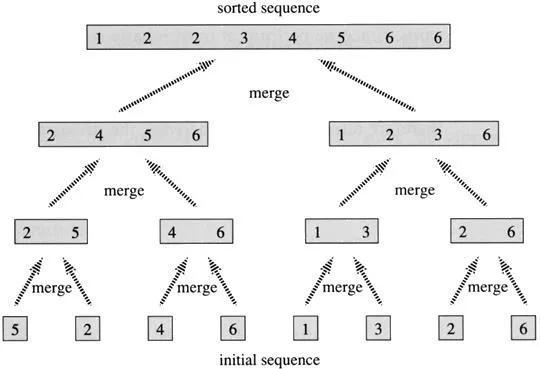
Once we have sorted the two or lesses, we need to MERGE each pair of two or lesses into arrays of size four (or less).

Take a look at the picture above again. Do you understand what I mean by merging? Did you bring your head right up to the screen to examine the second line closely? Regardless of your answer, look at it again and imagine merging the two size arrays into the four size arrays above them.

If the first element in the left array is smaller than the first of the right array, put the left's first element in the first spot of the four array, now look at the second element of the left array, but keep looking at the right. Put the smaller one in. Now you're looking at the last element of each two array. Put the smaller one in, that's 5 on the left side of the diagram. Now you have no more values to merge in that left two array, so tack on the rest of that right two array if it still has values to be merged.

You keep merging the pieces until you have the entire array.

Okay, look at that video. Note that it does the left side first before doing anything for the right side. This is because of how recursion is used. All of the mergesort(left)s will be executed before it ever gets to a mergesort(right) on the same level.

Time Complexity

Merge Sort has an O(n * log n ) worst-and best-case time complexity.

Ruby Implementation

Pastebin link; screenshot:

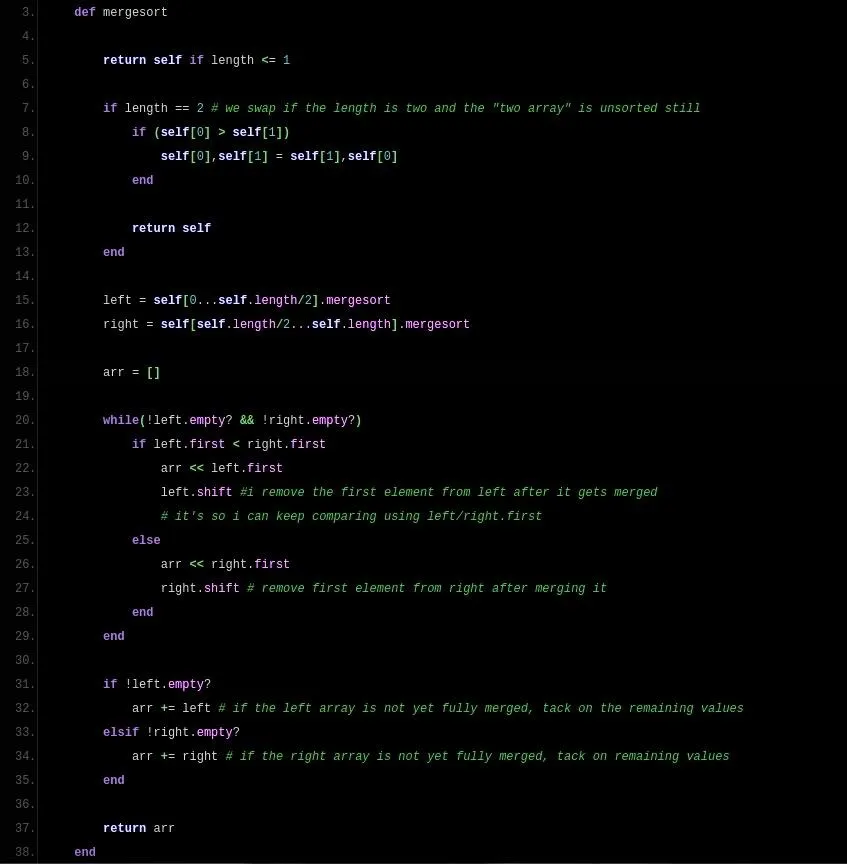
Lines 5 through 12 are the exit conditions, since we use recursion in mergesort() (because we call the function within itself on lines 15 and 16).

In this implementation, I extended Ruby's Array class to have a mergesort() method. That's why I call it with dot-notation.

If the array we are mergesorting has more than two elements, we call mergesort on its left and right halves right away (lines 15 and 16). No merging takes place until the array-to-sort self gets cut down into little two or less pieces. After that, we start merging.

I make an empty array arr to hold the result (line 18). Then, on line 20, I say while left and right both have elements, merge. The merging takes place in that while loop. I do it by comparing the smallest element of left to that of right. The smaller element of the two gets "merged" by appending it to arr. Then, we delete that element from left or right (where it came from) by calling Array#shift on lines 23 and 27.

We get to line 31 after either left or right is emptied out. We append the non-empty array. Note: only one array will have remaining elements at this point, and it'll be guaranteed that the result is sorted.

We then return the new array, arr.

C++ Version

Pastebin; screenshots (it's a two-image gallery):

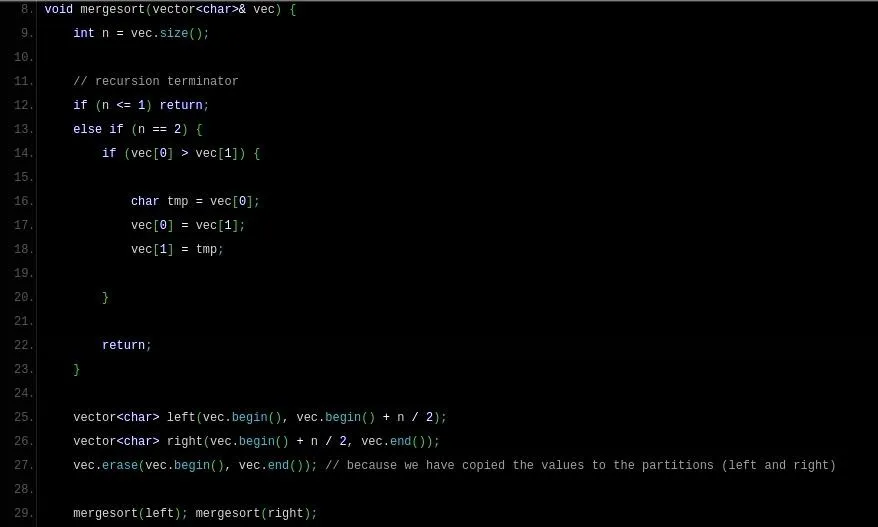
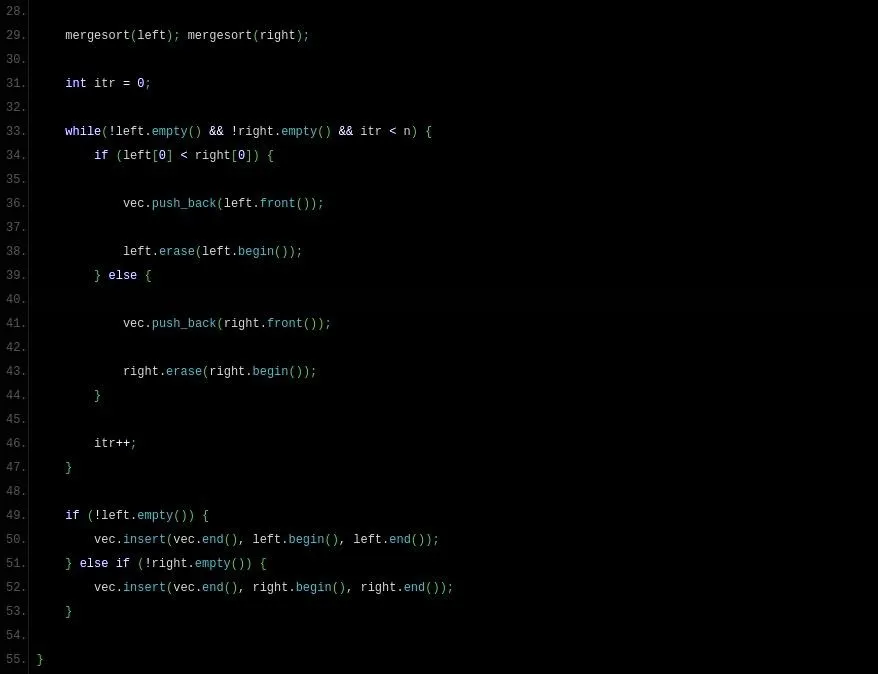
We do fundamentally the same thing, except that I didn't extend vector as I extended Array in the Ruby version. It's just a regular old function. Use the annotations I have provided above; otherwise, I've done all I can to explain Merge Sort.

Conclusion

That's it for this article. The implementations above are great on time, but a little heavier on memory than I'd like, so Merge Sort may make a return to NB in the future, a little wiser, a little more optimized.

Again, stay tuned for the optimization(s) of Quick Sort to come.

Comment below if you have a special sorting algorithm you'd like included in my series.

Stay sorted,
oaktree